Подсчет числа p методом Монте-Карло
Есть более простой способ статистического расчета числа p, чем тот, который использовал Бюффон. Можно нарисовать квадрат, вписать в него круг («квадратура круга») и бросать туда камешки. Так как в площади круга запрятано число p («пи эр в квадрате» – вспомним старый анекдот о том, почему у поезда колеса стучат), то через подсчет попаданий в круг можно оценить число p. Бюффон этот метод не использовал наверное из-за того, что трудно добиться равномерного попадания камешков в квадрат.
На рис. 3.6 зафиксирована оценка площади круга, вписанного в квадрат, и сделана попытка расчета значения числа p. Как это делалось?
В пункте 1 на рис 3.6 формируются два вектора X и Y, элементы которых (а их 7000) ¾ случайные вещественные числа в интервале от минус до плюс единицы. X и Y – это по своей сути координаты точек случайного падения камешков в квадрат размером 2 на 2. Далее в пункте 2 эти камешки сортируются на «чистых и нечистых»: координаты точек, попавших в круг, дублируются в векторах Xo и Yo (o ¾ попал), а не попавших ¾ в векторах Xx и Yx (x ¾ промах). После этого несложно визуализировать попадание точек в круг с помощью параметрического декартового графика. Достаточно при форматировании графика указать, что линий нет, а есть одни точки. При этом точки, попавшие в круг (вектора Xo и Yo), более толстые. Теперь для оценки числа p можно подсчитать число попаданий камешков в круг (пункт 4) ¾ число ненулевых элементов вектора Xo (или Yo). В пункте 5 число p рассчитывается и сравнивается с его точным значением.
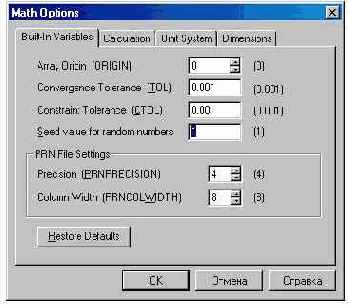
Функция rnd в среде Mathcad имеет аргумент, отличающийся от своих аналогов на языках программирования. В среде BASIC или Pascal аргумент функции rnd связан с приставкой псевдо- в ее названии, а не с диапазоном генерируемых случайных чисел. Да, числа генерируются случайные, но ряд этих чисел псевдослучаен, так как его в любой момент можно повторить. За такой повтор на языках программирования отвечает аргумент функции rnd, а в среде Mathcad – число (по умолчанию это 1), хранящееся в окне Seed value for random numbers (инициализация генератора случайных чисел) ярлыка Built-in Variables окна Math Options, которое вызывается на дисплей командой Options в меню Math:
От истинно случайных чисел отказались еще на заре развития компьютерной техники, когда пытались встраивать в ЭВМ что-то похожее на рулетку. Но это устройство оказалось слишком неповоротливым, а главное, с его помощью невозможно было получать повторяющиеся ряды случайных (псевдослучайных) чисел, что необходимо при отладке программ. Поэтому генерированию случайных чисел на физических моделях (рулетка) предпочли их математическое моделирование. Какой алгоритм заложен в функцию rnd, пользователя волнует мало – главное, чтобы ряд генерируемых чисел не вырождался, а сами числа распределялись в заданном диапазоне равномерно[4], в чем можно убедиться визуально – см. пункт 3 рис. 3.6.
Наш подсчет числа p методом Монте-Карло (а рулетка была не зря упомянута) – это чистой воды извращение (пардон, деривация): то же число p (или интеграл) легко можно рассчитать напрямую – конец пункта 5. Но все-таки наше извращение было не таким уж извращенным.
Во-первых, решив задачу на рис. 3.6, мы, по сути, не рассчитали значение p, а проверили качество генератора псевдослучайных чисел, то есть добротность встроенной функции rnd. При числе бросаний «камешков в воду», стремящемся к бесконечности, ошибка метода Монте-Карло должна стремиться к нулю, если функция rnd работает правильно.
Во-вторых, есть фигуры, площади которых невозможно рассчитать традиционными методами, без «извращений». Пример – площадь облака на снимке из космоса. Эту площадь довольно точно и, главное, быстро (в метеорологии вчерашний прогноз никому не нужен) можно определить, ткнув случайным образом несколько раз в фотографию иголкой, и… см. рис. 3.6.
Традиционные способы подсчета площади фигуры (интеграла) тут не годятся не только потому, что контуры облака невозможно описать какой-либо интегрируемой функцией, но и из-за того, что они размытые, нечеткие.
В математике, самой точной на свете науке, появилось новое направление: теория нечетких множеств (другой термин – «размытые множества», но по-английски это звучит более поэтично: «fuzzy sets» – пушистые множества[5]). Эта теория оперирует такими «перлами», как «скорее 1, чем 2», «скорее плюс, чем минус», «точка находится скорее под графиком, чем над ним» и т.д. В основе теории нечетких множеств лежит знаменитый софизм: «Если к горсти зерна добавить еще одно зернышко, превратится ли она в кучу? А если добавить два зерна? А сколько зерен превратят горсть в кучу?» Это самое сколько
– типичный представитель fuzzy set, к которому трудно приложить и современную теорию чисел, и саму цифровую вычислительную технику. Программирование же – это по своей сути жонглирование нулями и единицами, то есть крайняя категоричность мироощущения, когда все богатство цветов и оттенков сводится к черному и белому. Мир же состоит не из чисел, а из куч, горстей, облаков, то есть из нечетких множеств, к обсчету которых современные компьютеры приспособлены очень плохо. Кто поднимался на самолете сквозь облака, знает, что никакой границы между облаком и не облаком нет. В этом-то, по-видимому, и будет заключаться один из будущих кризисов теории программирования и вообще элементной базы компьютеров. К теории нечетких множеств мы еще вернемся в конце этого этюда в главке о четкой и нечеткой логике и в этюде 6. А пока задание читателю – реализовать в среде Mathcad метод подсчета числа p, предложенный Бюффоном.
Поэтому повторяю – наше извращение на рис. 3.6. было не таким уж извращенным.
Можно сказать, что на рис. 3.6. мы, подражая Казимиру Малевичу, нарисовали «Черный круг в черном квадрате». Так мы невольно вторглись в Мир Искусства…
Считается, что искусство зиждется на трех китах. Вот они: чувство меры, воображение и ... потребность в извращениях, связанная с сомнениями и творчеством.
Теперь о сомнениях.
