Оценка качеств менеджера (окончание)
Средневзвешенная оценка качества менеджера в баллах (пункт 4 на рис. 4.17) ¾ Kм = 4.162.
Алгоритм определения весовых коэффициентов ai влияет на оценку качества, которая может быть выполнена по выбору ЛПР на основе гипотезы равной значимости весовых коэффициентов:
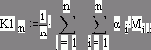
где ai = 1 / n.
В этом случае оценка качества значительно возрастает (в сравнении со средневзвешенной оценкой) – K1м
= 4.593.
Значения весовых коэффициентов могут быть установлены с учетом специфики конкретного заказа из условия приоритета качеств (требуется «высокий» профессионал, личность приятная во всех отношениях, но без особой склонности к руководству). В этом случае приоритеты могут быть установлены, например, на следующих значениях: для профессиональных качеств ¾ kп1=1.15, личностных ¾ kп2 =1.05, деловых ¾ kп3 =0.8. Значения весовых коэффициентов для групп качеств r определяются формулой:
(ar)i = kпr / n, где n = 9, r= 1, 2, 3,
и равны – (a1)i =
1.15 / 9 = 0.128; (a2)i = 1.05 / 9 = 0.117; (a3)i = 0.8 / 9 = 0.089.
Вектор-строка весовых коэффициентов имеет вид:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||
| (ar)I | (a1)i | (a1)i | (a1)i | (a2)i | (a2)i | (a2)i | (a3)i | (a3)i | (a3)i |
Средневзвешенная оценка качества менеджера в баллах (пункт 8 на рис. 4.17) ¾
Kм
= 4.496.
Итак, в рассмотренном примере в зависимости от способа определения весовых коэффициентов получены три оценки качества:
Km = 4.162 – при экспертной оценке a;
K1m
= 4.593 – случай равнозначимых весовых коэффициентов;
K2m = 4.496 – при приоритете (kп1=1.15) профессиональных качеств.
Выбор кандидата – прерогатива лица, принимающего решение, или конкурсной комиссии.
Рассмотренная методика применима для оценки качества продукции, результатов испытаний, экзаменов и других задач экспертной оценки.
Возможно, руководителю группы экспертов или заказчику экспертизы потребуется анализ результатов работы экспертов для оценки их компетентности, пристрастий или добросовестности.
Весовые коэффициенты i-го качества в оценке j-го эксперта рассчитываются по формуле
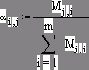
Результаты расчета содержатся в матрице a (пункт 5 на рис. 4.17).
Для наглядного представления результатов работы экспертов, анализа оценок, близости объекта к эталону качества в некоторых задачах очень удобна радарная диаграмма (Radar-diagram). Пример – экспертиза проекта электростанции по таким показателям: экономичность, экологичность, архитектурные решения, совместимость с еще не подпорченным ландшафтом, безопасность, надежность, значимость для экономики региона и др. Для всех показателей из центра диаграммы проводятся лучи, на которых откладываются средние значения оценок экспертов. Соединив точки на лучах, получим многоугольник. Эталону качества будет соответствовать вписанный в окружность с радиусом М (М – высший балл по шкале оценок) правильный многоугольник[17]. Степень приближения к эталону наглядно представляется формой и относительной площадью получившегося на основе оценок экспертов многоугольника (пункт 2 на рис. 4.6).
Тема оценки качества далеко не исчерпана. Интересные решения могут быть получены с использованием теории нечетких множеств (см. этюд 6).
[1] Сравните пары римских и арабских чисел на рис. 6.47.
[2] В среде Mathcad при форматировании чисел допустимо менять систему счислений. Двоичная система появилась только в Mathcad 8.
[3] Для поддержки АСНИ существуют также и специализированные программные средства – LabVIEW, LabWindows (разработка National Instruments, Corp.), например.
[4] Здесь лучше записать не нуль, а системную (предопределенную) переменную ORIGIN. Так мы и поступим в пункте 3.2 на рис. 4.2.
[5] Здесь чаще используют термин «аппроксимация» – приближение прямой линии к точкам. Еще здесь упоминают регрессию
– зависимость средней величины (прямая линия) от других величин (экспериментальные точки). Тут можно усмотреть некую путаницу в терминологии. Надеемся, что читатель в данном случае сам разберется, что к чему.
[6] Третья группа инструментов решения задач – это команды меню.
[7] Градация на линейную и нелинейную аппроксимацию весьма условна.
[8] Вот здесь-то и пригодятся средства символьной математики (этюд 7).
[9] На него нужно предварительно поместить курсор.
[10] Студенты автора называют ее «тормозная бабушка».
[11] Операторы функции, формируемых на рис. 4.10 и 4.13, объединены в единый операторный блок. Это позволяет использовать механизм локальных переменных – см. этюд 6.
[12] Автор советов – преподаватель Московского энергетического института. Основа не только российской, но и мировой энергетики – это теплоэнергетика (ТЭС и АЭС), где рабочее тело – в основном, вода и водяной пар.
[13] Если создаваемая функция будет использоваться для решения обратной задачи (поиск, например, значения температуры при заданных значениях давления и энтальпии пара), то такие сообщения об ошибке лучше убрать. При численном поиске корня уравнения (а к этому сводится такая задача) ничего не будет страшного в том, что мы временно будем вылезать из области разумного существования аргументов.
[14] Главка написана совместно с М.Панько.
[15] Понятие «эталон качества»- синоним оценки «высочайшее качество».
[16] Существенный недостаток данной методики в том, что все эксперты обязаны оценить все без исключения качества испытуемого. Мы должны заполнить прямоугольную таблицу – матрицу. Но в реальной жизни далеко не все привлеченные к этой работе являются признанными экспертами в оценке всех качеств объекта исследования. Мы уже сталкивались с подобной проблемой, втискивая табличные данные по энтальпии пара в квадратную матрицу – см. рис. 4.10.
[17] Вспомним чеховское: «В человеке все должно быть прекрасно – и лицо, и одежда, и душа, и мысли!»
